Castling-ViT: Compressing Self-Attention via Switching Towards Linear-Angular Attention During Vision Transformer Inference

Haoran You1,2,*, Yunyang Xiong2,*, Xiaoliang Dai2, Bichen Wu2, Peizhao Zhang2,
Haoqi Fan2, Peter Vajda2 Yingyan Lin1
1Georgia Institute of Technology, 2Meta Reality Labs
Paper Code
Interpolate start reference image.

Castling-ViT over SOTA baselines on image classification and object detection.

Abstract

Vision Transformers (ViTs) have shown impressive performance but still require a high computation cost as compared to convolutional neural networks (CNNs), due to the global similarity measurements and thus a quadratic complexity with the input tokens. Existing efficient ViTs adopt local attention (e.g., Swin) or linear attention (e.g., Performer), which sacrifice ViTs' capabilities of capturing either global or local context.

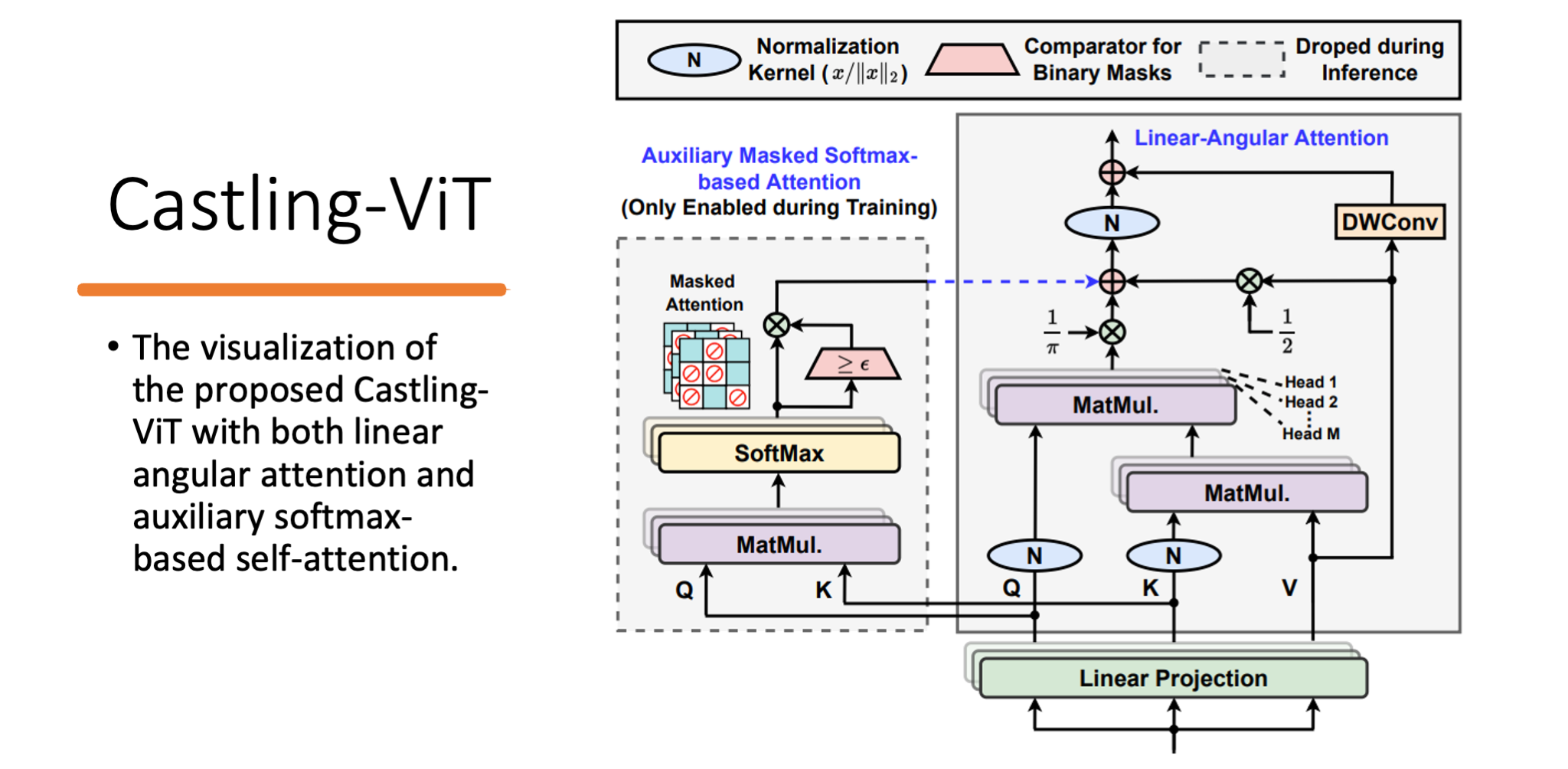
In this work, we ask an important research question: Can ViTs learn both global and local context while being more efficient during inference? To this end, we propose a framework called Castling-ViT, which trains ViTs using both linear-angular attention and masked softmax-based quadratic attention, but then switches to having only linear-angular attention during ViT inference. Our Castling-ViT leverages angular kernels to measure the similarities between queries and keys via spectral angles. And we further simplify it with two techniques:

(1) a novel linear-angular attention mechanism: we decompose the angular kernels into linear terms and high-order residuals, and only keep the linear terms; and (2) we adopt two parameterized modules to approximate high-order residuals: a depthwise convolution and an auxiliary masked softmax attention to help learn both global and local information, where the masks for softmax attention are regularized to gradually become zeros and thus incur no overhead during ViT inference.

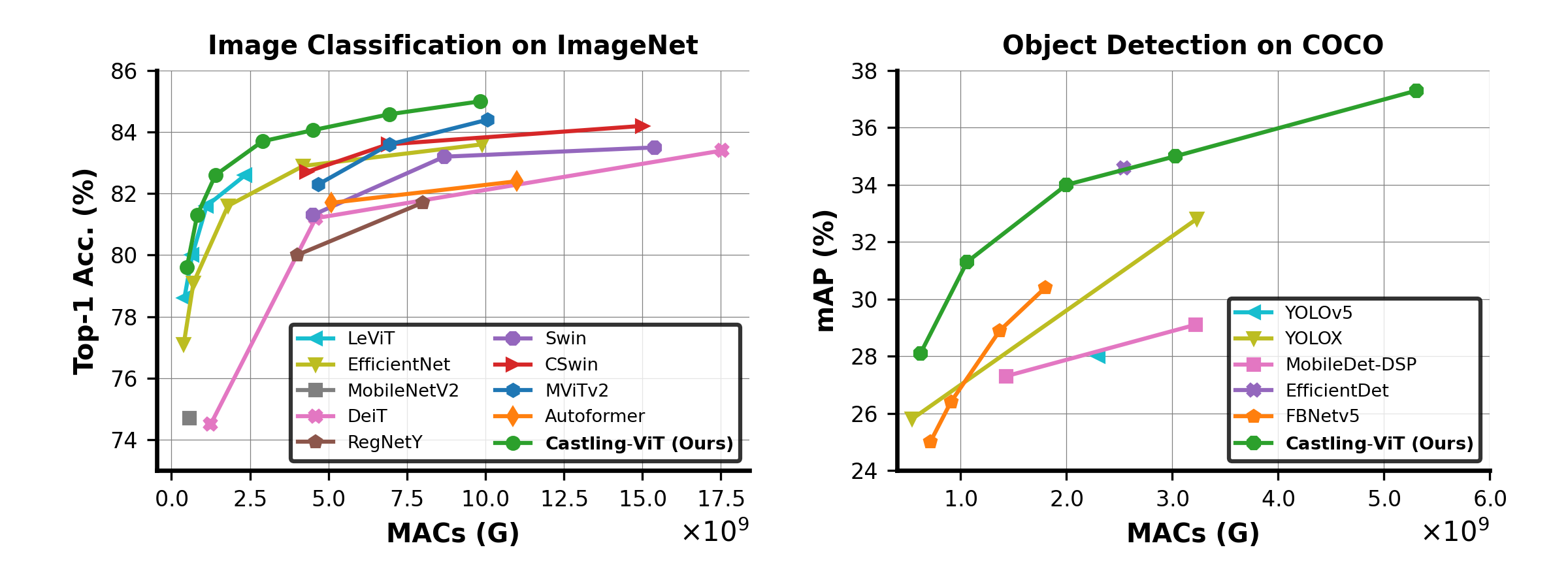
Extensive experiments and ablation studies on three tasks consistently validate the effectiveness of the proposed Castling-ViT, e.g., achieving up to a 1.8% higher accuracy or 40% MACs reduction on ImageNet classification and \textbf{1.2} higher mAP on COCO detection under comparable FLOPs, as compared to ViTs with vanilla softmax-based attentions.



Method

The below figure illustrates an overview of the proposed Castling-ViT, which makes linear attention more powerful than previous designs while still being efficient during inference.


Interpolate start reference image.

Core Implementation


class LinAngularAttention(nn.Module):
    def __init__(
        self,
        in_channels,
        num_heads=8,
        qkv_bias=False,
        attn_drop=0.0,
        proj_drop=0.0,
        res_kernel_size=9,
        sparse_reg=False,
    ):
        super().__init__()
        assert in_channels % num_heads == 0, "dim should be divisible by num_heads"
        self.num_heads = num_heads
        head_dim = in_channels // num_heads
        self.scale = head_dim**-0.5
        self.sparse_reg = sparse_reg

        self.qkv = nn.Linear(in_channels, in_channels * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(in_channels, in_channels)
        self.proj_drop = nn.Dropout(proj_drop)

        self.kq_matmul = MatMul()
        self.kqv_matmul = MatMul()
        if self.sparse_reg:
            self.qk_matmul = MatMul()
            self.sv_matmul = MatMul()

        self.dconv = nn.Conv2d(
            in_channels=self.num_heads,
            out_channels=self.num_heads,
            kernel_size=(res_kernel_size, 1),
            padding=(res_kernel_size // 2, 0),
            bias=False,
            groups=self.num_heads,
        )

    def forward(self, x):
        N, L, C = x.shape
        qkv = (
            self.qkv(x)
            .reshape(N, L, 3, self.num_heads, C // self.num_heads)
            .permute(2, 0, 3, 1, 4)
        )
        q, k, v = qkv.unbind(0)  # make torchscript happy (cannot use tensor as tuple)

        if self.sparse_reg:
            attn = self.qk_matmul(q * self.scale, k.transpose(-2, -1))
            attn = attn.softmax(dim=-1)
            mask = attn > 0.02 # note that the threshold could be different; adapt to your codebases.
            sparse = mask * attn

        q = q / q.norm(dim=-1, keepdim=True)
        k = k / k.norm(dim=-1, keepdim=True)
        dconv_v = self.dconv(v)

        attn = self.kq_matmul(k.transpose(-2, -1), v)

        if self.sparse_reg:
            x = (
                self.sv_matmul(sparse, v)
                + 0.5 * v
                + 1.0 / math.pi * self.kqv_matmul(q, attn)
            )
        else:
            x = 0.5 * v + 1.0 / math.pi * self.kqv_matmul(q, attn)
        x = x / x.norm(dim=-1, keepdim=True)
        x += dconv_v
        x = x.transpose(1, 2).reshape(N, L, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

BibTeX

@inproceedings{you2023castling,
  title={Castling-ViT: Compressing Self-Attention via Switching Towards Linear-Angular Attention During Vision Transformer Inference},
  author={You, Haoran and Xiong, Yunyang and Dai, Xiaoliang and Wu, Bichen and Zhang, Peizhao and Fan, Haoqi and Vajda, Peter and Lin, Yingyan},
  booktitle={The IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2023)},
  year={2023}
}